FRICTION
LIMITING FRICTION:
The maximum value of friction which comes into play when a body is just on the point of motion over the other body, is known as limiting friction.
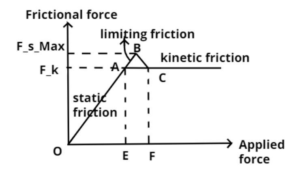
As shown, the applied force,F is increased from O to E, the frictional force is increased from O to Fs in the direct proportion. During the static condition, the frictional force increases in accordance with the applied force. A certain stage is reached when the applied force is just sufficient to overcome friction and motion of the body is about to take place. After the motion has taken place, the friction also suddenly decreases from Fs to Fk which remains constant throughout the movement period. The reason for the decrease of this friction is because there is very small time for the perfect interlocking of the protuberances of the surfaces. When the motion is just to commence, maximum friction is encountered. This condition is known as Limiting Equilibrium. The friction acting at this stage is termed as Limiting Friction.
LAWS OF FRICTION:
-
Laws of Friction for Static:
- Force of friction always act in a direction opposite to that in which the body tends to move.
-
- The force of friction depends upon the nature of the surfaces in contact.
-
- The force of friction is independent of the area of contact between the two surfaces.
-
- The magnitude of the force of friction is exactly equal to the applied force.
-
- The magnitude of the maximum static friction bears a constant ratio to the normal reaction between the two surfaces.
-
Laws of Friction for Dynamic:
- Force of friction always act in a direction opposite to that in which the body tends to move.
-
- The dynamic friction bears a constant ratio to the normal reaction between the two surfaces.
-
- The force of friction remains constant for moderate speeds. But it decreases slightly with the increase of speed.
CO-EFFICIENT OF FRICTION:
The ratio of limiting friction and the normal reaction is called co-efficient of friction. The frictional force depends upon the normal reaction on the contact surfaces and the nature of the two surfaces. For any set of two materials, friction is dependent upon the normal reaction. Higher the value of the normal reaction, greater will be the friction.
Let R = Normal reaction
and F = Force of friction (limiting friction)
therefore, F ∝ R
or [frac up=”F” down=”R”] = constant = μ
The ratio of limiting friction and normal reaction is called co-efficient of friction and is denoted by μ.
μ = [frac up=”F” down=”R”]
μ is a unit less quantity. Mostly the value of μ is less than one.
There are two values of μ.
When there is limiting equilibrium, the coefficient of friction is called static an is denoted by μs.
When the bodies are in relative motion, the coefficient of friction is called Kinetic and is denoted by μk.
Coefficient of friction between different materials.
| S. No. | MATERIAL | CO-EFFICIENT OF FRICTION (μ) |
| 1 | Cast Iron on Cast Iron | 0.16 |
| 2 | Mild Steel on Mild Steel | 0.14 to 0.19 |
| 3 | Wood on Wood | 0.32 to 0.6 |
| 4 | Leather on Cast Iron | 0.56 |
| 5 | Rope on Wood | 0.70 |
| 6 | Leather on Wood | 0.37 to 0.48 |
| 7 | Wood on Metal | 0.3 to 0.7 |
| 8 | Rubber on Dry Asphalt | -1 |
| 9 | Rubber on Wet Asphalt | 0.95 |
| 10 | Steel in Ice | 0.010 |
| 11 | Rubber on Ice | 0.005 |
ANGLE OF FRICTION:
The maximum angle between the normal reaction and resultant of force of limiting friction and normal reaction is known as angle of friction. When the limiting equilibrium is reached i.e., the body is just about to move, the limiting frictional force F and the normal reaction R, can be compounded to give a resultant S. The angle α which this resultant makes with the normal reaction R, is called the angle of friction.
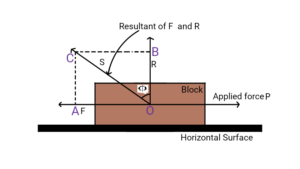
Let,
P = Applied force on the block
R = Normal Reaction
S = Resultant of frictional force and normal reaction
F = Frictional Force
Φ = Angle of Friction
Mathematically,
tan Φ = [frac up=”F” down=”R”]
Φ = tan˜¹ [frac up=”F” down=”R”]
As we know, [frac up=”F” down=”R”] = μ
From the above discussion, we get
tan Φ = μ
Φ = tan˜¹ μ
ANGLE OF REPOSE:
Angle of repose is the maximum angle of inclination of the plane at which a body remains in equilibrium under the action of friction only.
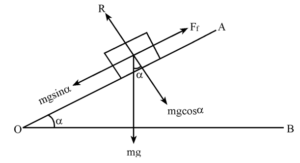
Consider a block of weight W (mg) resting in an inclined plane. The angle of inclination of the plane with the horizontal is α. If the angle of inclination is increased gradually, such that the block is just at the point of sliding down. At this position the block is in equilibrium under the action of following forces:
- Weight of the block, W (mg)
- Normal Reaction, R
- Frictional Force, F
Resolving all the forces parallel and perpendicular to the plane,
R = W cos α (i)
F = W sin α (ii)
Dividing (i) and (ii) we get
[frac up=”W sin α” down=”W cos α”] = [frac up=”F” down=”R”]
tan α = [frac up=”F” down=”R”]
tan α = μ
α = μ
Angle of Repose = Angle of Friction
RELATED VIDEOS FOR LAWS OF FRICTION:
