EXPERIMENT
OBJECTIVE:
To determine the velocity ratio, mechanical advantage and efficiency of a single threaded worm and worm wheel.
APPARATUS REQUIRED:
Worm and worm wheel apparatus, weight, string, scale etc.
THEORY:
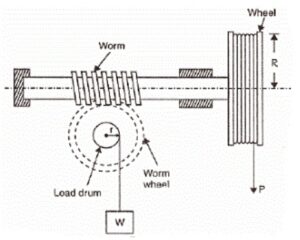
- Worm gears are gears which are widely used for transmitting power at high velocity ratios between non-intersecting shafts that are generally, but not necessarily at right angles.
- It is used to transmit power at high velocity ratios 300:1.
- Many worm gears have an interesting property that no other gear set has: the worm can easily turn the gear, but the gear cannot turn the worm.
- These are widely used in material handling and transportation machinery, machine tools, automobiles etc.
- It is a multi start threaded geared system.
- It consists of a square threaded screw and a toothed wheel geared with each other.
- A wheel is attached to the worm gear, over which passes a rope, a load is securely mounted on the worm wheel.
Let,
R = Radius of the effort wheel
r = Radius of the load drum
W = Load lifted
P = Effort applied to lift the load
T = Number of teeth on the worm wheel
In the first revolution of wheel , distance moved by effort = 2πr, as worm is single threaded.
The load drum will move through [frac up=”1″ down=”T”]
Distance, through which the load will move = [frac up=”2πr” down=”T”]
VELOCITY RATIO (V.R) = [frac up=”Distance moved by effort” down=”Distance moved by load drum”]
MECHANICAL ADVANTAGE (M.A) = [frac up=”Load” down=”Effort”] or [frac up=”W” down=”P”]
EFFICIENCY = [frac up=”Mechanical Advantage” down=”Velocity Ratio”] x 100 or [frac up=”M.A” down=”V.R”] x 100
PROCEDURE:
- Measure the radius of the effort wheel and load drum with the help of string.
- Count the number of teeth on worm wheel.
- Wrap the string over the effort wheel and load drum.
- Suspend some load to the spring passing over the load drum via hanger and go on adding weight in the pan.
- Note the effort in the weight pan.
- Calculate the mechanical advantage.
- Calculate the velocity ratio.
- Repeat the experiment with different loads.
OBSERVATION TABLE:
| S. No. | Load Drum 2πr (in cm) |
Effort Drum 2πR (in cm) |
No. of teeth on worm wheel (T) |
Load Lifted (W) (in grams) |
Weight of pan (P1) (in grams) |
Weight added in pan (P2) (in grams) |
Total Effort P= P1+P2 (in grams) |
M.A = [frac up=”W” down=”P”] | V.R = [frac up=”2πrRT” down=”2πr”] | Efficiency = [frac up=”M.A” down=”V.R”] x 100 |
PRECAUTIONS:
- Lubricate the bearings of to decrease friction.
- Weight should be gently placed in effort pan.
- String should not overlap on pulley.
- String should not be loose on pulley.
- The pan carrying weight should not be touched.
- There should not be any knot in the string.
- Note down the readings carefully.
Applications of Worm Gears
Tuning Instruments – most guitars, basses, banjos and other stringed instruments use a worm gear for the tuning mechanism to work. The gear’s force reduction is the main reason for this, coupled with the locking capability that keeps the desired string tightness in place. This type of worm gear is different to most as you can tune both up and down; whereas most worm gears can only be turned in one direction.
Elevators/Lifts – worm gears can often be found in the machinery of common elevators/lifts because of their compact size and non-reversible properties. As the gear/load cannot transmit motion back through the worm/hoist, using this type of gear can act as a secondary braking system. This means the load cannot free fall and load speed is easily regulated.
RELATED VIDEOS:
