LAWS OF MOTION
The Law of Conservation of Momentum states when a system of interacting objects is not influenced by outside forces (like friction), the total momentum of the system cannot change.
RECOIL OF GUN
It is an example of law of conservation of momentum.
When a bullet is fired from a loaded gun, then according to Newton’s third law of motion, reaction of the bullet (which will act opposite to the direction of the fire) acts on the gun. As a result the gun moves backward with some velocity and hence the person who fires the gun experiences a jerk or impact. This backward movement of the gun is called Recoil of Gun.
Let
m = mass of the bullet
M = Mass of the gun
v = Velocity of the bullet
V = Velocity of the gun
Before firing both the gun and the bullet is at rest and the velocity is zero. Thus, Initial momentum = 0
Momentum gained by the bullet = mv
Momentum of the gun = MV
Thus, final momentum = mv + MV
According to law of conservation of momentum,
Initial momentum = Final momentum
0 = mv + MV
V = – [frac up=”mv” down=”M”]
D’ALEMBERT’S PRINCIPLE
It states that “Similar to the equations of static equilibrium, equation of dynamic equilibrium can also be established by introducing inertia force in the direction opposite to the acceleration in addition to the real forces.
As we know that the equations of static equilibrium are
ΣH = 0, Σv = 0, ΣM = 0
Similarly when different external forces act on a body in motion, the algebraic sum of all the forces is zero.
As we know, F = ma
where,
F= Force acting on the moving body
m = Mass of the body
a = Acceleration of the body
F = ma
F – ma = 0
F +(-ma) = 0
The above equation is called the equation of dynamic equilibrium under the action of real force F. The expression in the bracket of the equation is the inertia force and negative sign shows that it acts in a direction opposite to that of the real force.
MOTION OF A LIFT
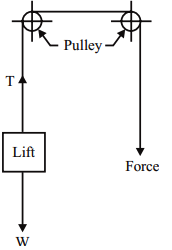
Consider a lift moving with a uniform acceleration carrying some mass.
Let,
m = Mass carried by the lift
a = Uniform acceleration of the lift
W = Weight carried by the lift = mg
T = Tension in the cable supporting the lift
WHEN THE LIFT IS MOVING UPWARD
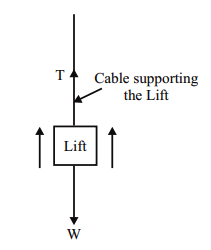
The net upward force which causes the upward motion of the lift is = T – W
Also the net upward force = Mass x Acceleration = m x a
m x a = T – W
T = W + ma
T = mg + ma
T = m (g+a)
WHEN THE LIFT IS MOVING DOWNWARD
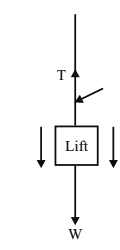
The net downward force which causes the motion in the lift is = W – T
Also the net downward force = Mass x Acceleration = m x a
m x a = W – T
T = W – ma
T = mg – ma
T = m (g-a)
RELATED VIDEOS:
