POLYGON

Polygon is a plane figure bounded by many (usually five or more) straight lines.

When all the sides and included angles are equal, it is called as a REGULAR POLYGON.

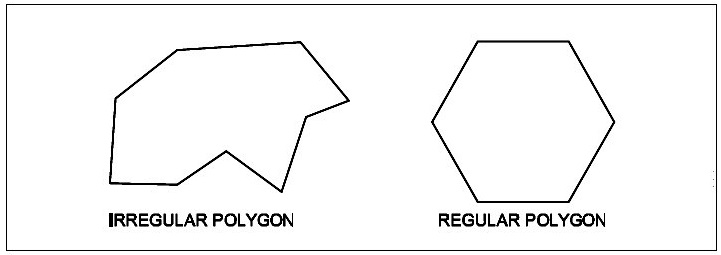
When all the sides and included angles are unequal, it is called IRREGULAR POLYGON.

Polygons are named in terms of their number of sides as given below:

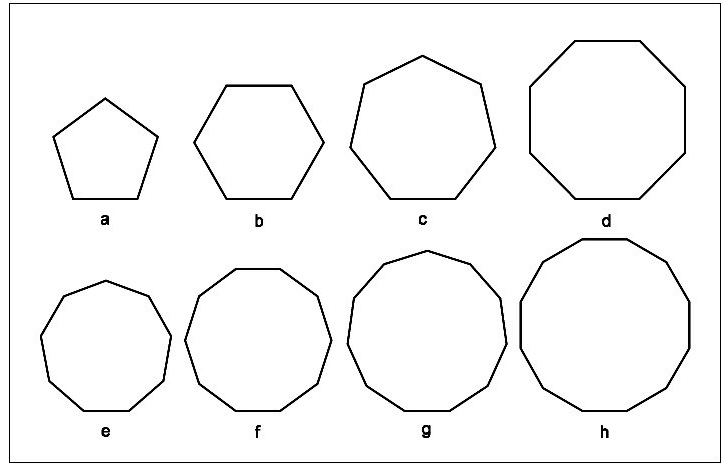
S. No.	NAME	NUMBER OF SIDES
a	PENTAGON	5
b	HEXAGON	6
c	HEPTAGON	7
d	OCTAGON	8
e	NONAGON	9
f	DECAGON	10
g	UNDECAGON	11
h	DUODECAGON	12

PROPERTIES OF POLYGON:

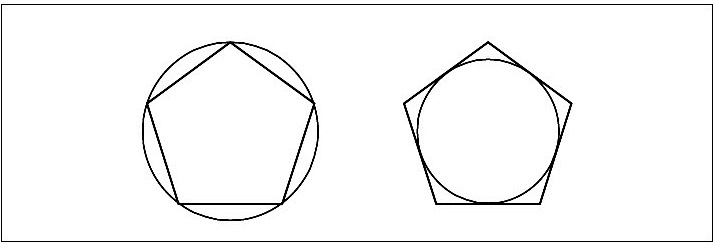
All corners of a regular polygon lie on the circle. The sides of a regular polygon will be tangential to the circle drawn in side.

The sum of the interior angles of a polygon is equal to (2 x n – 4) x right angle, where n is the number of sides.

The sum of exterior angles of a polygon is equal to 360°.

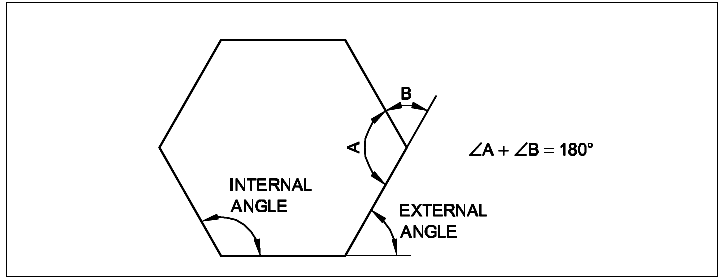
The sum of the interior angle and the corresponding external angle is 180°.

Draw a regular heptagon of side 25 mm.

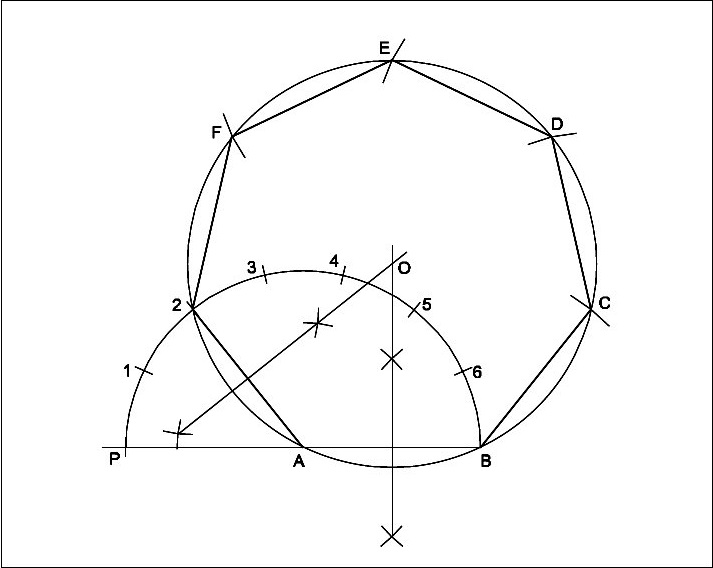
Semi-circular method

Draw a line AB equal to 25 mm.

Extend BA to a convenient length.

`A’ as centre and radius AB describe a semi-circle.

Divide the semi-circle into seven equal parts (number of sides) using divider.

Number the points as 1,2,3,4,5,6 starting from `P’.

Join A2

Draw the perpendicular bisectors from 2A and AB intersecting at 0.

`0′ as centre and OA or OB as radius describe a circle.

Mark the points C,D,E,F and 2 on the circle such that BC = CD = DE = EF = F2 = AB.

Join the line BC, CD, DE, EF and F2.

ABCDEF2 is required heptagon.

Semi-circle method

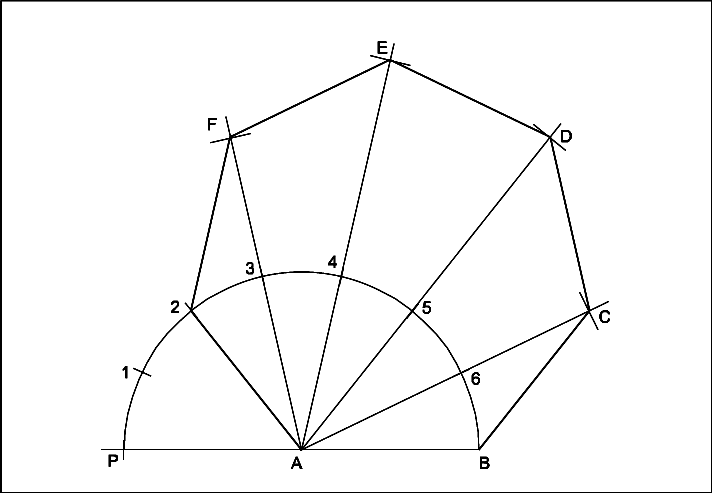
Follow the procedure upto dividing the semi-circle into number of equal parts.

Join A2.

Join A3, A4, A5 and A6 and extend to a convenient length.

With centre `B’ and radius AB draw an arc cutting A6 extended line at `C’.

`C’ as centre and same radius, draw an arc cutting the line A5 at `D’.

Locate the points E & F in the same manner.

Join BC, CD, DE, EF and F2.

ABCDEF2 is the required heptagon.

Draw a Pentagon inside a circle of diameter 60 mm.

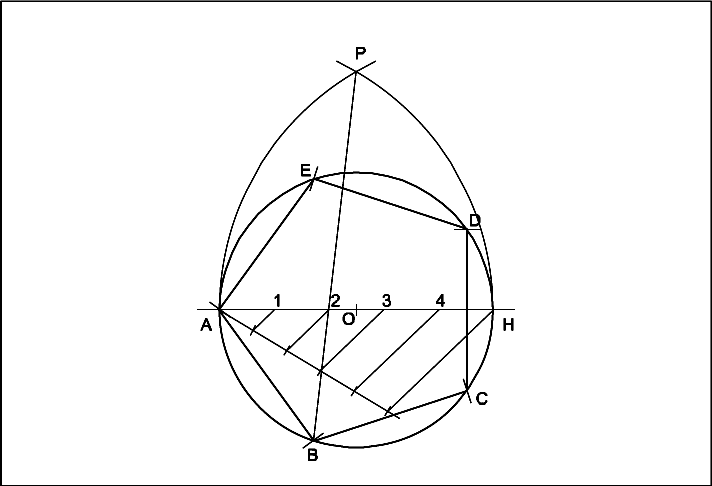
Draw the line AH equals to 60 mm. (Diameter of circle).

`O’ as centre OA as radius describe a circle.

Divide AH into 5 equal parts (as many equal parts as the sides).

A and H as centres, AH as radius describe arcs intersecting at `P’.

Join P2 and extend it to meet the circle at `B’.

Set off BC, CD, DE, EF equals to AB on the circle.

Join the points.

ABCDEF is the required pentagon.

Draw a Hexagon (Circumscribing) of side 32 mm by Arc Method.

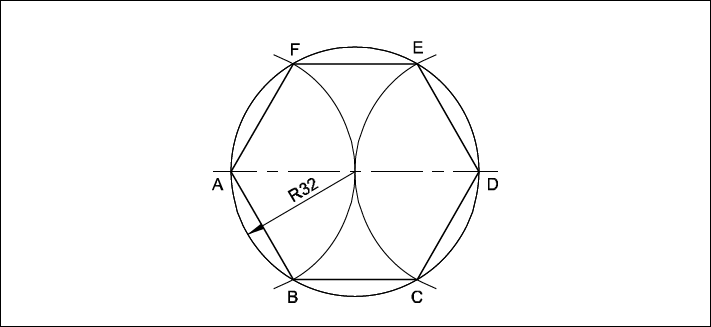
Draw a circle of radius 32 mm.

Mark the diameter AD.

With same radius, A and D as centres. draw two arcs cutting the circle at points B,F,E & C respectively.

Join AB, BC, CD, DE, EF and FA.

ABCDE is the required hexagon.

Draw a Hexagon inside a circle of diameter 60 mm (inscribing).

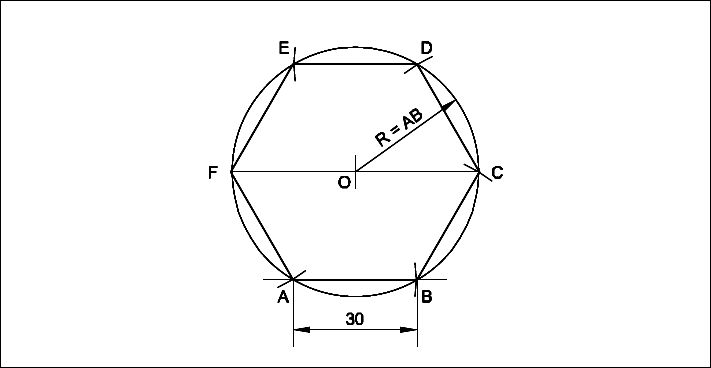
Draw a line FC equal to 60 mm (Diameter of circle).

‘O’ as centre describe a circle on the diameter FC.

F as centre FO as radius draw an arc at A.

‘A’ as centre, same radius draw an arc at B.

In the same manner set the points C,D & E.

Join AB, BC, CD, DE, EF and FA.

ABCDEF is the required hexagon.

Draw a Hexagon with Across Flat Method.

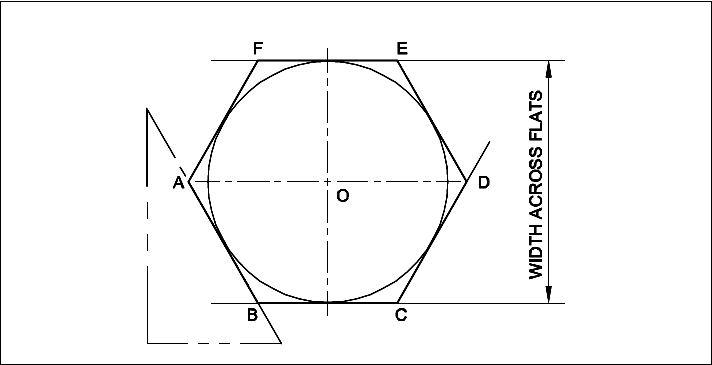
Hexagon, distance across flat of 45 mm

Draw a circle of Φ 45. (45 mm is the size across flat).

Draw two horizontal tangents BC and FE.

With 60° setsquare draw four tangents, touching the horizontal tangents.

Mark the corners A,B,C,D,E and F.

ABCDEF is the required hexagon.

ENGINEERING DRAWING- Polygon